ACTOR, in collaboration with a main luxury cruise company, has developed the Magellano Project, aiming to take advantage of optimization methods in the decision making for cruise itineraries planning.
The project
In its decision making process, a cruise company must face three levels of decision problems:
– at a strategic level, the deployment of the fleet, that is to decide in which maritime area and in which season window to locate each ship of its fleet;
– at a tactical level, given a ship in a maritime area, in a season window, to establish which cruises to offer to the customers, where each cruise is characterized by the embarkation port, the disembarkation port and the cruise length (in days);
– at an operational level, given a cruise, namely embarkation port, disembarkation port and number of days, to determine the day-by-day itinerary, in terms of transit ports, arrival and departure times in transit ports, and so on.
This project focuses both on the tactical level and on the operational level.
At the tactical level, we consider the problem of scheduling cruises with the objective to maximize the expected revenue provided by a given ship located in a specified maritime area, in a selected season window, taking into account a number of constraints:
- any disembarkation port is the embarkation port of the next cruise, except for the first one and the last one of the season;
- for any port a minimum and a maximum number of possible visits is fixed;
- a port cannot be visited again, unless a minimum number of days is elapsed after the last visit;
- for any cruise length, a minimum and a maximum number of cruises to be scheduled are given;
- some cruise must depart/arrive in a given port, in a given day of the season (cruise with a milestone);
- some cruise specified by departure port/day, arrival port/day, must be included (charter cruise).
Constraint 1 is a continuity constraint; constraints 2, 3 and 4 clearly aim at offering a catalogue of cruises differentiated enough among them; constraint 5 is due to some event that a cruise must meet in some port; constraint 6 is due to corporate buying of a cruise. The expected revenue is estimated from past records of cruises in the same maritime areas and by the same or similar ships. Moreover, forecasts on the cruise market trend are also taken into account. We propose an Integer Linear Programming (ILP) model for this scheduling problem.
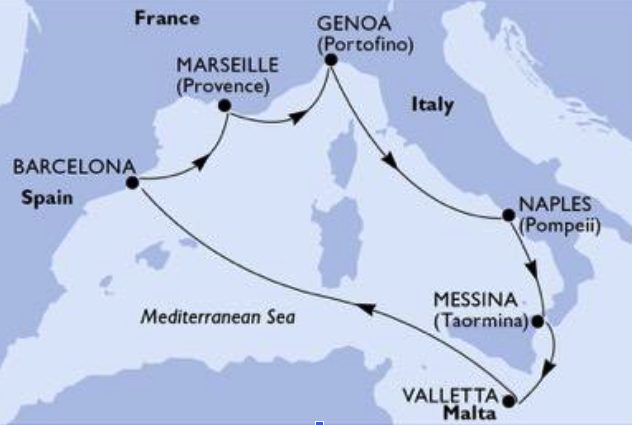
At the operational level we determine the day-by-day itinerary in terms of transit ports and arrival and departure times, with the objective of minimizing the itinerary cost due to fuel and port costs, and maximizing an attractiveness index of the itinerary. This latter is related to the ports visited and the number of days spent at sea, i.e. without docking in a port. Therefore the problem turns out to be a bi-objective optimization problem.
As to the first objective, the fuel consumption depends nonlinearly on the ship speed; the speed depends on the distances between the ports and the need to meet times for entering and leaving the port; the port cost depends on the port location and on the services provided. As to the second objective, it is evaluated by giving a rating to each port, to the days spent at sea (when the travel time between two successive ports exceeds 24 hours) and to overnights in port. Operational constraints are due to minimum and maximum number of transit ports to be visited, to the allowable time windows for arrival and departure in the port, to minimum and maximum time of stay in each port, to the fact that some ports may be obliged or prohibited, or may be visited only in given days, to minimum and maximum number of days spent at sea.
We propose a bi-objective Mixed Integer Linear Programming (MILP) model for this problem. We provide its solution in terms of points of the Pareto frontier obtained by using two “a posteriori” methods: the method of weights and the method of constraints. Each Pareto optimal solution provides the optimal day-by-day itinerary, in terms of ports to be visited and times of arrivals and departures.
We coded all mathematical models of the Magellano Project by using the AMPL language and we used the GUROBI solver to compute all optimal solutions.

Awards
The Magellano Project has been awarded by AIRO, the Italian Association of Operations Research, as the best application of Operations Research developed in Italy in 2015.
References
Cruise itineraries optimal scheduling
A two-objective optimization of ship itineraries for a cruise company

